Modelica.Blocks.Continuous.LimPID

P, PI, PD, and PID controller with limited output, anti-windup compensation and setpoint weighting

Information

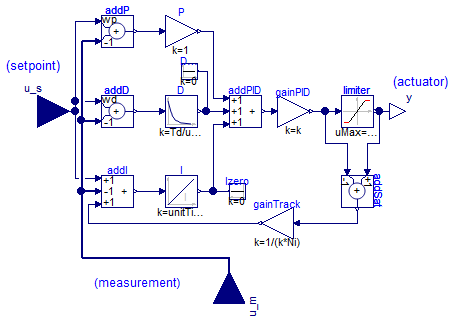
Via parameter controllerType either P, PI, PD, or PID can be selected. If, e.g., PI is selected, all components belonging to the D-part are removed from the block (via conditional declarations). The example model Modelica.Blocks.Examples.PID_Controller demonstrates the usage of this controller. Several practical aspects of PID controller design are incorporated according to chapter 3 of the book:

Åström K.J., and Hägglund T.:

PID Controllers: Theory, Design, and Tuning. Instrument Society of America, 2nd edition, 1995.

Besides the additive proportional, integral and derivative part of this controller, the following features are present:

• The output of this controller is limited. If the controller is in its limits, anti-windup compensation is activated to drive the integrator state to zero.
• The high-frequency gain of the derivative part is limited to avoid excessive amplification of measurement noise.
• Setpoint weighting is present, which allows to weight the setpoint in the proportional and the derivative part independently from the measurement. The controller will respond to load disturbances and measurement noise independently of this setting (parameters wp, wd). However, setpoint changes will depend on this setting. For example, it is useful to set the setpoint weight wd for the derivative part to zero, if steps may occur in the setpoint signal.

The parameters of the controller can be manually adjusted by performing simulations of the closed loop system (= controller + plant connected together) and using the following strategy:

1. Set very large limits, e.g., yMax = Modelica.Constants.inf
2. Select a P-controller and manually enlarge parameter k (the total gain of the controller) until the closed-loop response cannot be improved any more.
3. Select a PI-controller and manually adjust parameters k and Ti (the time constant of the integrator). The first value of Ti can be selected, such that it is in the order of the time constant of the oscillations occurring with the P-controller. If, e.g., vibrations in the order of T=10 ms occur in the previous step, start with Ti=0.01 s.
4. If you want to make the reaction of the control loop faster (but probably less robust against disturbances and measurement noise) select a PID-Controller and manually adjust parameters k, Ti, Td (time constant of derivative block).
5. Set the limits yMax and yMin according to your specification.
6. Perform simulations such that the output of the PID controller goes in its limits. Tune Ni (Ni*Ti is the time constant of the anti-windup compensation) such that the input to the limiter block (= limiter.u) goes quickly enough back to its limits. If Ni is decreased, this happens faster. If Ni=infinity, the anti-windup compensation is switched off and the controller works bad.

Initialization

This block can be initialized in different ways controlled by parameter initType. The possible values of initType are defined in Modelica.Blocks.Types.InitPID. This type is identical to Types.Init, with the only exception that the additional option DoNotUse_InitialIntegratorState is added for backward compatibility reasons (= integrator is initialized with InitialState whereas differential part is initialized with NoInit which was the initialization in version 2.2 of the Modelica standard library).

Based on the setting of initType, the integrator (I) and derivative (D) blocks inside the PID controller are initialized according to the following table:

In many cases, the most useful initial condition is SteadyState because initial transients are then no longer present. If initType = InitPID.SteadyState, then in some cases difficulties might occur. The reason is the equation of the integrator:

   der(y) = k*u;

The steady state equation "der(x)=0" leads to the condition that the input u to the integrator is zero. If the input u is already (directly or indirectly) defined by another initial condition, then the initialization problem is singular (has none or infinitely many solutions). This situation occurs often for mechanical systems, where, e.g., u = desiredSpeed - measuredSpeed and since speed is both a state and a derivative, it is natural to initialize it with zero. As sketched this is, however, not possible. The solution is to not initialize u_m or the variable that is used to compute u_m by an algebraic equation.

If parameter limitAtInit = false, the limits at the output of this controller block are removed from the initialization problem which leads to a much simpler equation system. After initialization has been performed, it is checked via an assert whether the output is in the defined limits. For backward compatibility reasons limitAtInit = true. In most cases it is best to use limitAtInit = false.

Extends from Interfaces.SVcontrol (Single-Variable continuous controller).

Parameters

Connectors

Modelica definition

Modelica.Blocks.Continuous.Integrator

Output the integral of the input signal

Information

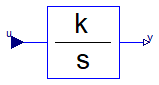
This blocks computes output y (element-wise) as integral of the input u multiplied with the gain k:

         k
     y = - u
         s

It might be difficult to initialize the integrator in steady state. This is discussed in the description of package Continuous.

Extends from Interfaces.SISO (Single Input Single Output continuous control block).

Parameters

Connectors

Modelica definition

Modelica.Blocks.Continuous.LimIntegrator

Integrator with limited value of the output

Information

This blocks computes y (element-wise) as integral of the input u multiplied with the gain k. If the integral reaches a given upper or lower limit and the input will drive the integral outside of this bound, the integration is halted and only restarted if the input drives the integral away from the bounds.

It might be difficult to initialize the integrator in steady state. This is discussed in the description of package Continuous.

If parameter limitAtInit = false, the limits of the integrator are removed from the initialization problem which leads to a much simpler equation system. After initialization has been performed, it is checked via an assert whether the output is in the defined limits. For backward compatibility reasons limitAtInit = true. In most cases it is best to use limitAtInit = false.

Extends from Interfaces.SISO (Single Input Single Output continuous control block).

Parameters

Connectors

Modelica definition

Modelica.Blocks.Continuous.FirstOrder

First order transfer function block (= 1 pole)

Information

This blocks defines the transfer function between the input u and the output y (element-wise) as first order system:

               k
     y = ------------ * u
            T * s + 1

If you would like to be able to change easily between different transfer functions (FirstOrder, SecondOrder, ... ) by changing parameters, use the general block TransferFunction instead and model a first order SISO system with parameters
b = {k}, a = {T, 1}.

Example:
   parameter: k = 0.3, T = 0.4
   results in:
             0.3
      y = ----------- * u
          0.4 s + 1.0

Extends from Interfaces.SISO (Single Input Single Output continuous control block).

Parameters

Connectors

Modelica definition

Modelica.Blocks.Continuous.Derivative

Approximated derivative block

Information

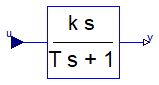
This blocks defines the transfer function between the input u and the output y (element-wise) as approximated derivative:

             k * s
     y = ------------ * u
            T * s + 1

If you would like to be able to change easily between different transfer functions (FirstOrder, SecondOrder, ... ) by changing parameters, use the general block TransferFunction instead and model a derivative block with parameters
b = {k,0}, a = {T, 1}.

If k=0, the block reduces to y=0.

Extends from Interfaces.SISO (Single Input Single Output continuous control block).

Parameters

Connectors

Modelica definition